Kunci Jawaban
Rangkuman Materi Matematika Kelas 8 SMP Bab 2 Kurikulum Merdeka, Pembahasan Teorema Pythagoras
Di bawah ini disediakan ringkasan seputar Teorema Pythagoras dari Bab 2 Kurikulum Merdeka. Simak rangkuman materi selengkapnya berikut ini.
Penulis: Tria Agustina | Editor: Tria Agustina
SRIPOKU.COM - Simak rangkuman materi Matematika berikut ini.
Di bawah ini disediakan ringkasan seputar Teorema Pythagoras dari Bab 2 Kurikulum Merdeka.
Materi ini dirangkum guna memudahkan siswa kelas 8 SMP dalam belajar.
Dilansir lewat YouTube Portal Edukasi, simak rangkuman materi yang ditampilkan berikut ini sebagai panduan pembelajaran.
Baca juga: Rangkuman Materi Matematika Kelas 9 SMP BAB 3 Kurikulum Merdeka, Pembahasan Transformasi Geometri
Rumus Pythagoras
Pada suatu segitiga siku-siku, luas persegi pada sisi miringnya sama dengan jumlah luas persegi lain pada kedua sisi sikusikunya, hal ini juga berarti jumlah dari kuadrat kedua sisi siku-siku segitiga pada segitiga siku-siku sama dengan kuadrat panjang sisi miringnya (hipotenusa).
Berdasarkan dalil tersebut kita bisa menyimpulkan bahwa rumus pythagoras pada segitiga siku-siku adalah:

Rumus ini berlaku untuk segitiga siku-siku dan mencari sisi terpanjangnya. Bagaimana menentukan sisi terpanjangnya? Caranya adalah melihat sisi yang berhadapan dengan sudut siku-siku itu sendiri.
Ada dua cara, cara mudah dan cara buku.
Cara buku dengan menggunakan kebalikan dari teorema Pythagoras.
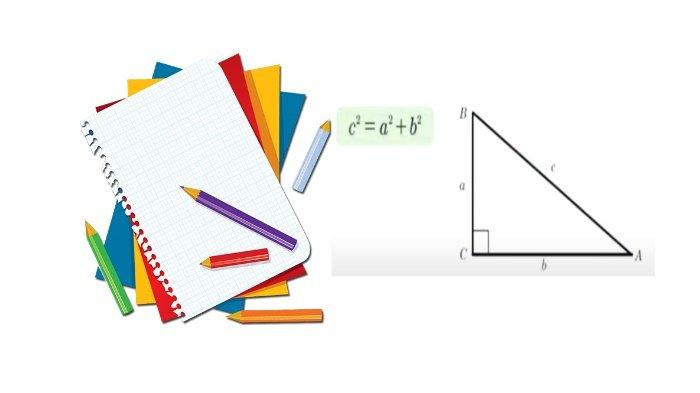
Seperti gambar ini:

Tinggal lihat mana yang tegak lurus seperti huruf L, nah itu siku- sikunya, maka yang berhadapannya adalah sisi terpanjangnya.
Jika diketahui alas sebuah segitiga siku-siku 5cm dan tingginya 12 cm, tentukan sisi terpanjang pada segitiga tersebut! Maka jawabannya adalah:

Contoh lain, jika diketahui sisi terpanjang pada segitiga siku-siku 2,9 cm dan tingginya 2,1 cm, tentukan alas segitiga tersebut!
Maka jawabannya adalah:

Baca juga: Rangkuman Materi Matematika Kelas 9 SMP Bab 2 Kurikulum Merdeka, Pembahasan Bangun Ruang Sisi Datar
Tripel Pythagoras
Tripel pythagoras sebenarnya untuk memudahkan kita dalam menghitung karena bisa dihafalkan. Jadi tidak perlu repot-repot lagi menghitung.
Berikut ini adalah daftar tripel pythagoras.

Semua nya itu berurutan ya a, b, dan c.
Contoh:
Diketahui sebuah segitiga siku-siku memiliki alas 696 cm dan tinggi 697 cm. Tentukan sisi terpanjangnya!
Jawabannya berdasarkan di tabel adalah 985 cm.
Segitiga Istimewa
Segitiga istimewa yang pertama adalah segitiga siku-siku sama kaki.
Segitiga siku-siku sama kaki adalah segitiga istimewa yang ukuran ketiga sudutnya adalah 45° - 45°-90°. Ketika menemukan segitiga siku-siku sama kaki, maka sisi terpanjangnya tinggal ditambahkan √2.
Diketahui sebuah segitiga memiliki alas dan tinggi 5 cm, tentukan sisi terpanjangnya!
Maka otomatis jawabannya adalah 5/2 cm.
Lalu yang kedua adalah segitiga yang memiliki sudut 30° - 60°-90°. Ketika menemukan segitiga seperti ini maka berlaku aturan:

Bisa kalian lihat bahwa:
• Sisi yang berhadapan dengan sudut 30 derajat besarnya 1x
• Sisi yang berhadapan dengan sudut 90 derajat besarnya 2x
• Sisi yang berhadapan dengan sudut 60 derajat besarnya tinggal ditambahkan 3 dari panjang terkecil.
Jadi misalkan contohnya, sambil lihat gambar diatas ya: Diketahui panjang AB adalah 4cm, tentukan panjang BC dan AC! Langsung ketahuan bahwa:
• Panjang BC = setengah dari panjang AB maka = 4 : 2 = 2cm
• Panjang AC = tinggal tambahin 3 dari panjang BC maka = 2/3 cm.
Contoh lain:
Diketahui panjang AC adalah 100/3 cm, tentukan panjang AB dan BC!
Langsung ketahuan bahwa:
• Panjang BC = tinggal dihilangin 3 dari panjang AC maka = 100 cm.
• Panjang AB = dua kali panjang BC maka = 2 x 100 = 200 cm.
Dapatkan konten pendidikan mata pelajaran lainnya dari Kurikulum Merdeka dengan klik Di Sini
Dapatkan juga berita penting dan informasi menarik lainnya dengan mengklik Google News
| Latihan Soal STS Bahasa Indonesia Kelas 10 SMA Semester 1, Dilengkapi Kunci Jawaban + Indikator Soal |

|
|---|
| Latihan Soal Pendidikan Pancasila Kelas 10 SMA Bab 1 Halaman 46 Kurikulum Merdeka Uji Kompetensi 1.4 |

|
|---|
| Soal Informatika Kelas 9 SMA BAB 3 Hal 45-48 Kurikulum Merdeka, Teknologi Informasi dan Komunikasi |

|
|---|
| Kunci Jawaban Ekonomi Kelas 11 SMA Halaman 18-19 Kurikulum Merdeka Edisi Revisi, Soal Aktivitas 4.7 |

|
|---|
| Soal IPAS Kelas 5 SD Bab 2 Halaman 43-47 Harmoni dalam Ekosistem Kurikulum Merdeka, Mari Refleksikan |

|
|---|















Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.